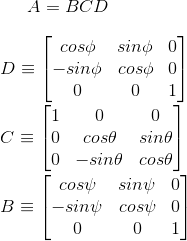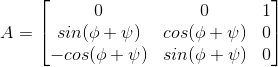Euler Angles
An amateur astronomer was staring into the dark, shiny night sky. Far away from usual hustle-bustle of the city and its pollution clouded sky, he was trying to locate some stars on his sophisticated telescope. He had a list of stars and some numbers scribbled onto a sheet of paper. Against each star, he had written two values- an azimuth angle and an angle of elevation or altitude. To direct to a point in a 3D space, after all, two ‘rotation’ values should suffice. You first indicate the azimuth angle (angle swept on a horizontal reference plane starting from a reference line on it). Then the elevation angle tells how high above this horizontal plane you ‘lift’.
Now if he were to locate an airplane instead (it is quite unlikely that he would find one in that desolate paradise of his!) he would require another ‘rotation’ value to specify its orientation. Think of it, just pointing to the airplane as if it were a star will not tell the direction it is travelling in. That validates the necessity for a third parameter. The lesson learnt from the story is this- for completely specifying the orientation of an ‘extended object’ like the airplane with respect to a reference frame, three rotation parameters are a minimum.
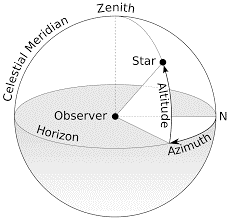
Where does this come into the satellite picture? Remember, the attitude of a satellite (an ‘extended’ object) gives its (more specially, its body frame’s) orientation with respect to a reference frame. And this requires three rotation parameters. Euler angles captures this idea. This is a set of three ‘ordered’ rotation parameters. So, each parameter corresponds to rotation about a specific axis the new coordinate system obtained post rotation. Each rotation is mathematically represented by a rotation matrix. And matrix multiplication of three rotation matrices (again, order is important) gives the net rotation.
Shown above is a rotation following a particular convention of (Ф,Ө,ψ), the angles being rotation about (z,x,z) axes respectively. The rotation matrix A then is,[1]
Euler angles, however, entails some limitations. Firstly, these values are not obvious. One cannot guess them by merely looking at the final orientation. Think of it, when you are restricted by convention to use a particular sequence of axis rotations, you have to in some sense have some ‘foresight’ to understand the consequence of each rotation on the following one(s) and correctly predict the right combination of values. In the case of our amateur astronomer who had to point to an airplane, if we were to ask him to make a rotation to account for its orientation first before pointing to it he would’ve had a hard time. He wouldn’t know how his action of pointing to it (i.e the subsequent rotations) affect this initial adjustment he has made for its orientation.
Another major problem with euler angles is that of gimbal lock. If Ө=π/2 above, then final rotation matrix A would be:[2]
In the rotation we have made above, Ф and ψ have lost their unique identities. There are multiple values we could use to obtain the same result (as long as Ф +ψ is the same). Here, we have lost a degree of freedom, only two independent parameters are required to represent this rotation. In a mathematical sense, this is a problem, because we don’t have unique Ф and ψ values at hand.
Quaternions is an alternative to Euler angles. It uses the fact that one unique axis and a rotation about it can do this job. It is, in fact, more intuitive.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem