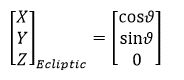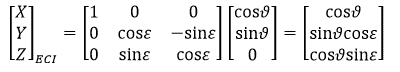Determination of Sun Vector using Sunsensors
Sun vector is useful in determining whether the satellite is in light region or the eclipse region. [1]
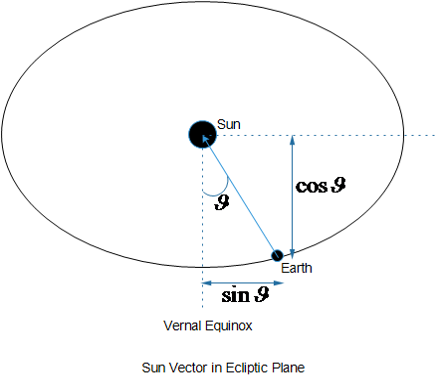
Sun vector is the vector from the center of earth to center of sun. Actually it is from the satellite to the sun but for all practical purposes we can assume it is from earth to sun (distance between earth and sun 149,597,870 km and earth and satellite around 700 km + radius of the earth for LEO satellites). Before dirtying our hands for the calculation, let’s look at how the equatorial plane and ecliptic planes are defined and what is vernal equinox.
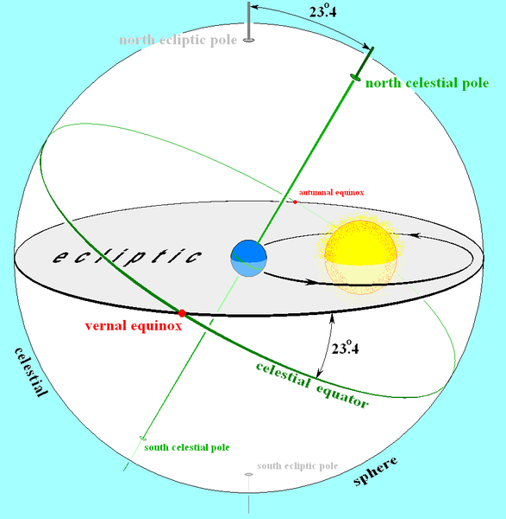
- Equatorial Plane: It is the plane perpendicular to the axis of rotation of earth. It is midway between North and South pole and divides the earth into two Hemispheres – Northern and Southern.
- Ecliptic Plane: The plane which is coplanar with the Earth’s orbit around Sun. The axis of Earth is tilted by 23.4 degrees with respect to this ecliptic plane. This tilt is the reason we have seasons.[2] Isn’t that Cool and Hot and Rainy?
- Vernal Equinox: The Vernal (Spring – around 21st March) Equinox in the Northern Hemisphere is the Autumnal (Fall- around 23rd September) Equinox in the Southern Hemisphere and vice versa. Since most of the countries are in the Northern Hemisphere, so in general we define the Vernal and Autumnal equinox with respect to Northern hemisphere.
The vernal equinox is one of two days in a year, when the earth has equal length of day and night. Why only two days? Why not all days? Blame it on the tilt of Earth’s axis. It’s a bit hard to imagine but at spring and fall the (in the Fig alongside) the northern and southern hemispheres receive the same amount of sunlight.
Enough of the preparatory material! Let’s now calculate the Sun Vector. The figure below is the top view of the ecliptic plane. In this plane the sun vector is from earth to sun and is making an angle ϑ from vernal equinox.
So the sun vector can be written as:
Since the ecliptic and equatorial planes have a tilt in between of 23.4 deg, we have to rotate the vector by this angle about X axis. So the Sun Vector in ECI frame becomes:
Determination of Light/Eclipse region
During the travel around the earth there comes a time when the satellite experiences some dark moments. This happens when the earth comes in between the sun and satellite. When this time comes and how long will it remain can be determined by simple geometry and our knowledge of sun vector.
Here we are defining the dark region as umbra and rest is taken as the light region. We wish to calculate how long will the satellite be in Umbra. You can see from the figure that umbra region is formed by simply drawing the common tangents of earth and sun.
Let’s define first some of the parameters first.
Rs = Radius of Sun.
Re = Radius of Earth.
r = Center distance between Earth and Sun.
ru = Distance between center of earth and apex of umbra.
α = Umbra apex half angle
θ = angle between satellite position vector (from earth) and sun vector.
∅ = angle between sun vector and the vector formed be apex of umbra and satellite.
ru can be calculated by forming similar triangle.
The region of umbra would be when it follows two conditions:
The knowledge of eclipse region is important from the power subsystem point of view. In this region there will no solar panel in the sunlight so the satellite functionalities have to depend solely on batteries. Also, in this region the sun vector can’t be calculated using the sun sensor. Any output coming on the sun sensor would be noise and we should not calculate sun vector using sun sensor in this region.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem