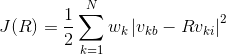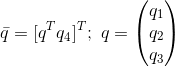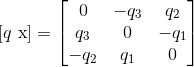Q Method and Wahba's Problem

TRIAD method is useful when we have only two vector measurements. If we need better accuracy and have more than two vector measurements, we need to use a more general algorithm. Before developing an algorithm, we need to make our problem statement more precise. Say we have N unit vectors [math]v_k[/math], k = 1,2...N. We have a sensor measurement in the body frame for each vector, [math]v_{kb}[/math], and a mathematical model of the components in the inertial frame, [math]v_{ki}[/math]. Our aim is to find a rotation matrix [math]R_{bi}[/math], such that

for each of the N vectors. It is clear that this set of equations will be overdetermined for N > 2, and hence the equation, in general, cannot be satisfied for each k = 1,2..N. Hence, we wish to find a solution for [math]R_{bi}[/math] that in some way minimizes the overall error for the N vectors.

In this expression, J is the loss function that has to be minimized, k is the counter for the N observations, [math]w_k[/math] is weight assigned to the kth measurement, [math]v_{kb}[/math] is the matrix consisting of the measured components in the body frame, and [math]v_{ki}[/math] is the matrix consisting of components in the inertial frame as determined using appropriate mathematical models. This loss function is a sum of the squared errors for each vector measurement. If the measurements and mathematical models are perfect, then J = 0, since the first equation on this page will be satisfied for all N vectors. If there are any errors or noisy measurements, then J > 0. The smaller we make J, the better the approximation of [math]R_{bi}[/math].

Q-Method

In this section we present one of the several methods to solve this minimization problem known as the Q-method. We first expand the loss function as

Assuming normalized vectors, we see that,

Defining,

We can see that in order to minimize J, we need to maximize g(R). This problem can be written in a better and more elegant way by representing rotation matrix R in terms of the quaternion

R can be written in terms of q as [math]R = (q_4^2-q^Tq)I+2qq^T-2q_4[q \times][/math]
Where [q x] is the cross product matrix associated with q

One can verify that the gain function in terms of the quaternions is: [math]g(\bar{q}) = \bar{q}^TKq[/math]
Where K is a 4x4 Matrix given by

Wherein,
[math]B = \sum w_k(v_{kb}v_{ki}^T)[/math]
[math]S = B+B^T[/math]
[math]Z = \sum w_k(v_{kb} \times v_{ki})[/math]
[math]\sigma = tr(B)[/math]

Now we want to maximise g. However, noting that quaternion elements are not independent, the constraint [math]\bar{q}^Tq = 1[/math] must also be satisfied. So we use the lagrangian multiplier method and differentiate with respect to [math]\bar{q}[/math] we get [math]K\bar{q} = \lambda \bar{q}[/math]. So now, we have reduced the problem to an eigenvalue problem for the matrix K. Since, K is a 4x4 matrix, it can have at most 4 different eigenvalues. Substituting [math]K\bar{q} = \lambda \bar{q}[/math] in [math]g(\bar{q}) = \bar{q}^TKq[/math], we get

Now we want to maximise g. So we will chose the eigenvector corresponding to the maximum eigenvalue. Hence the estimated attitude can be known by solving the eigenvalue problem for the matrix K.

---

If you are done reading this page, you can go back to Attitude Determination and Control Subsystem