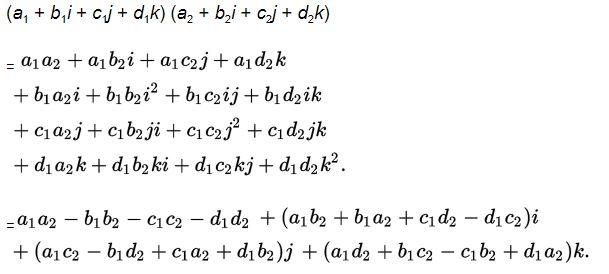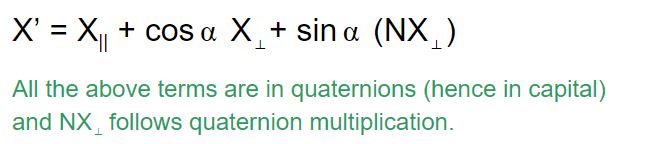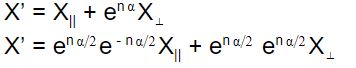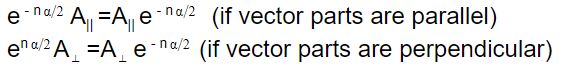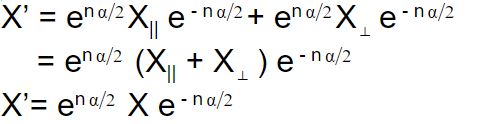Quaternions
“There are two types of geniuses. Ordinary geniuses do great things, but they leave you room to believe that you could do the same if only you worked hard enough. Then there are magicians, and you can have no idea how they do it.”
It is surprising how simplified mathematical modelling of rotations has become with the advent of quaternions. One can’t stop admiring how each of the properties of quaternions has a subtle role to play in accomplishing this task of rotation. And these seem to have been defined with a magical foresight that they would all somehow fit into place later.
Quaternions were constructed in attempt to extend the idea of rotations in a complex plane to 3D. Each quaternion is a set of four parameters. Why four? Well, any rigid body rotation can be done about a unique axis. So, 3 parameters to specify the axis and 1 for the angle rotated about it. But we have an endless choice of vectors along the axis to represent it. Here comes an applicational constraint from the fact that we want a rotation that doesn’t scale. So we restrict to unit quaternions (quaternions of unit magnitude). In retrospection, this has also simplified the mathematical design for rotation using quaternions.
So we’ll start with vector notation for rotation and make an attempt to build a mathematical construct for unit quaternions.

In the picture above, x is being rotated to x’ about n in anticlockwise sense. This is equivalent to keeping its component parallel to n preserved and rotating the perpendicular component. Mathematically this is given as,
Now, a general quaternion is written as a + b i + c j + d k (or equivalently (a,v)). ‘a’ is called the scalar part and the rest is the vector part (think of i,j,k to be similar to the unit orthogonal vectors of 3D space).
To proceed, we’ll define few quaternion properties, [1]
- Addition
- Magnitude
(where q* is the conjugate quaternion of q. It’s scalar part is the same but the vector part is multiplied with (-1) )
- Multiplication
This is done defining ij=k ; jk=i ; ki=j ; ii=jj=kk= -1; So, ijk=-1. Notice, this is defined in accordance with the right- handed cross product of vectors. This was deliberate (as will be evident when we use quaternions to represent the vector rotation equation above).
In short,
An useful observation here is that if above r1 =r2 =0 and v1 and v2 are perpendicular then
(0, v1)(0, v2)= (0, v1 X v2). {we are doing vector cross product in v1 X v2}
We’ll use this to update the vector rotation equation to quaternion notation. To extend vectors to quaternions, we’ll simply put the scalar part to zero and retain the vector notation in the vector part.
So, back to the rotation equation:
For unit quaternion multiplication with vector (in quaternion form),
The above can be directly verified from the rules of multiplication.
So finally,
The above equation is used to perform rotations using unit quaternions. All along, the requirement of preserving vector magnitude never explicitly forced us to choose unit quaternions. However, this has been ensured because we started with a vector equation that took this into account and unit quaternion was an output of subsequent manipulations of this equation.
Formulation of quaternions has made two major accomplishments. Firstly, it was able to give Euler’s rotation theorem (which says any rotation of a ‘rigid body’ is equivalent to a single rotation about a unique axis) a more solid mathematical application. Secondly, it was able to “mathematically” resolve the problem of gimbal lock (here's a nice video on gimbal lock) that euler angles face. It should be pointed out now that though quaternions provided a ‘mathematical’ alternative to euler angles, they didn’t fully dislodge them. For instance, there are still mechanical systems that perform successive rotations in a predefined manner to realise a final rotation. It is natural and convenient to describe these using euler rotation angles. Quaternions in this case can’t help circumvent the gimbal lock issue because the euler angles are a physical requirement. Quaternions are, hence, only a ‘mathematical’ antidote to gimbal lock. Nevertheless, they are a huge simplification of their existing mathematical counterparts.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem