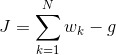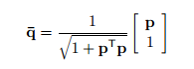Difference between revisions of "QuEST"
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | We had begun with the problem of overdetermination because we had more equations than the unknown variables. Now, with sensor errors it becomes impossible to solve for these variables such that it satisfies all the equations (remember, these equations are superfluous). So Wahba’s problem gives us a way to, if not circumvent, at least rationally deal with this problem. It defines a weighted error function (i.e errors from each of the sensors are given weightage based on reliability) which is to be minimised. | |
| − | |||
| − | |||
| − | + | [[File:Equation74.png|frame|center]] | |
| − | + | The error function J can be simplified to a summation involving <math>w_k</math> (the weights, which are constants set by us) and the gain function g as defined below | |
| − | [[File: | + | [[File:Equation75.png|frame|center]] |
| − | + | It is easy to see that minimising J is equivalent to maximising g. <br \> | |
| − | [[File: | + | This expression when written in terms of quaternions becomes very compact. And qmethod showed that maximising g involved solving an eigenvalue problem. This can be done on MATLAB or other computer tools. But the solution is numerically intensive.<ref>http://www.dept.aoe.vt.edu/~cdhall/courses/aoe4140/attde.pdf</ref> Satellite makers need a better algorithm than [[Q Method and Wahba's Problem| Q-method]] to determine the attitude with minimal compromise in the accuracy. The QuEST algorithm provides a less efficient but a ‘faster’ way to solve the eigenvalue problem.<br \> |
| − | + | QuEST starts with the assumption that sensor errors are minimal so that J can be minimised to a very low value. Rewriting J in terms of g, | |
[[File:Equation42.png|frame|center]] | [[File:Equation42.png|frame|center]] | ||
[[File:Equation43.png]] where [[File:Equation44.png]] is the maximum eigenvalue of the K matrix defined in [[Q Method and Wahba's Problem]]. | [[File:Equation43.png]] where [[File:Equation44.png]] is the maximum eigenvalue of the K matrix defined in [[Q Method and Wahba's Problem]]. | ||
| Line 15: | Line 13: | ||
If we approximate J to be very small (this approximation is valid as we want to minimize J and now if after completing this method, we calculate J, it would be very small), | If we approximate J to be very small (this approximation is valid as we want to minimize J and now if after completing this method, we calculate J, it would be very small), | ||
[[File:Equation46.png|frame|center]] | [[File:Equation46.png|frame|center]] | ||
| − | + | So, generally, QuEST uses Newton Raphson method starting with [[File:Equation44.png]] calculated above, and over multiple iterations reaches at a more accurate value for λ.<br \> | |
| − | [[File: | + | Notice how this is different from the qmethod. QuEST doesn’t directly solve for the eigen values. It starts with a reasonable guess and then moves on to check out if there are values close to this guess that can do better.<br \> |
| − | + | Now to solve for the quaternion, both scalar and vector parts are divided <math>q_4 =cos \frac{\phi}{2}</math> (<math>q_4</math> is the scalar part; <math> \phi</math> is the angle of rotation). Note, this only changes the magnitude of the quaternion and the final answer can be corrected for later by normalising it. So, the vector part now is <math>\boldsymbol{p} = \frac{\bar{\boldsymbol{q}}}{q_4} = a*tan\frac{\phi}{2}</math>, | |
| + | where <math>a</math> is the vector along axis of rotation. The initial matrix equation now turns out as follows | ||
[[File:Equation48.png|frame|center]] | [[File:Equation48.png|frame|center]] | ||
| − | + | '''p''' is being operated on by an invertible matrix. And Gauss elimination could be employed to find its inverse and hence solve for '''p'''. <br \> | |
| − | + | Finally, the quaternion is normalised to get an unit quaternion. | |
[[File:Equation49.png|frame|center]] | [[File:Equation49.png|frame|center]] | ||
| − | + | In general, while choosing between algorithm one has to make a tradeoff between getting a more accurate answer and implementing a computationally intensive code. QuEST adopts less accurate approach than qmethod at the cost of reducing computation.<br \> | |
| + | ---- | ||
If you are done reading this page, you can go back to [[Attitude Determination and Control Subsystem]] | If you are done reading this page, you can go back to [[Attitude Determination and Control Subsystem]] | ||
| + | == References == | ||
Latest revision as of 16:34, 19 February 2018
We had begun with the problem of overdetermination because we had more equations than the unknown variables. Now, with sensor errors it becomes impossible to solve for these variables such that it satisfies all the equations (remember, these equations are superfluous). So Wahba’s problem gives us a way to, if not circumvent, at least rationally deal with this problem. It defines a weighted error function (i.e errors from each of the sensors are given weightage based on reliability) which is to be minimised.
The error function J can be simplified to a summation involving (the weights, which are constants set by us) and the gain function g as defined below
It is easy to see that minimising J is equivalent to maximising g.
This expression when written in terms of quaternions becomes very compact. And qmethod showed that maximising g involved solving an eigenvalue problem. This can be done on MATLAB or other computer tools. But the solution is numerically intensive.[1] Satellite makers need a better algorithm than Q-method to determine the attitude with minimal compromise in the accuracy. The QuEST algorithm provides a less efficient but a ‘faster’ way to solve the eigenvalue problem.
QuEST starts with the assumption that sensor errors are minimal so that J can be minimised to a very low value. Rewriting J in terms of g,
![]() where
where ![]() is the maximum eigenvalue of the K matrix defined in Q Method and Wahba's Problem.
With this
is the maximum eigenvalue of the K matrix defined in Q Method and Wahba's Problem.
With this ![]() can be written as
can be written as
If we approximate J to be very small (this approximation is valid as we want to minimize J and now if after completing this method, we calculate J, it would be very small),
So, generally, QuEST uses Newton Raphson method starting with ![]() calculated above, and over multiple iterations reaches at a more accurate value for λ.
calculated above, and over multiple iterations reaches at a more accurate value for λ.
Notice how this is different from the qmethod. QuEST doesn’t directly solve for the eigen values. It starts with a reasonable guess and then moves on to check out if there are values close to this guess that can do better.
Now to solve for the quaternion, both scalar and vector parts are divided ( is the scalar part; is the angle of rotation). Note, this only changes the magnitude of the quaternion and the final answer can be corrected for later by normalising it. So, the vector part now is ,
where is the vector along axis of rotation. The initial matrix equation now turns out as follows
p is being operated on by an invertible matrix. And Gauss elimination could be employed to find its inverse and hence solve for p.
Finally, the quaternion is normalised to get an unit quaternion.
In general, while choosing between algorithm one has to make a tradeoff between getting a more accurate answer and implementing a computationally intensive code. QuEST adopts less accurate approach than qmethod at the cost of reducing computation.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem