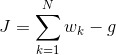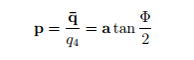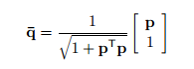Difference between revisions of "QuEST"
(Created page with "== Introduction == Obtaining quaternion information from q-method involves solving the eigenvalue problem for a 4X4 Matrix. This can be done on MATLAB or other computer tools....") |
|||
| Line 4: | Line 4: | ||
== The Algorithm == | == The Algorithm == | ||
| − | Recall from [[Q | + | Recall from [[Q Method and Wahba's Problem]] that the optimal attitude minimizes the loss function, |
[[File:Equation40.JPG|frame|center]] | [[File:Equation40.JPG|frame|center]] | ||
And maximizes the gain function, | And maximizes the gain function, | ||
| Line 10: | Line 10: | ||
Thus, | Thus, | ||
[[File:Equation42.png|frame|center]] | [[File:Equation42.png|frame|center]] | ||
| − | [[File:Equation43.png]] where [[File:Equation44.png]] is the maximum eigenvalue of the K matrix defined in [[Q | + | [[File:Equation43.png]] where [[File:Equation44.png]] is the maximum eigenvalue of the K matrix defined in [[Q Method and Whab's Problem]]. |
With this [[File:Equation44.png]] can be written as | With this [[File:Equation44.png]] can be written as | ||
[[File:Equation45.png|frame|center]] | [[File:Equation45.png|frame|center]] | ||
Revision as of 10:48, 25 January 2018
Introduction
Obtaining quaternion information from q-method involves solving the eigenvalue problem for a 4X4 Matrix. This can be done on MATLAB or other computer tools. But the solution is numerically intensive. On-board computing is a serious concern for any satellite designer and hence a better algorithm to solve this problem using less computing is required.
The QuEST algorithm provides a less efficient but a ‘faster’ way to solve the eigenvalue problem.
The Algorithm
Recall from Q Method and Wahba's Problem that the optimal attitude minimizes the loss function,
And maximizes the gain function,
Thus,
where 
is the maximum eigenvalue of the K matrix defined in Q Method and Whab's Problem.
With this can be written as
If we approximate J to be very small (this approximation is valid as we want to minimize J and now if after completing this method, we calculate J, it would be very small),
Defining and writing the equation in terms of Rodrigue’s parameter p simplifies the equation
where a is the vector along axis of rotation and Φ is the angle of rotation. Eigenvalue equation, which was to be solved is now written as
Which can be solved by gauss elimination.
Once the p has been obtained, the quaternion can be found out by noting
Hence the estimated quaternion is obtained without solving eigenvalue equation.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem
