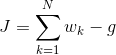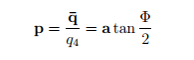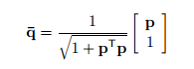We had begun with the problem of overdetermination because we had more equations than the unknown variables. Now, with sensor errors it becomes impossible to solve for these variables such that it satisfies all the equations (remember, these equations are superfluous). So Wahba’s problem gives us a way to, if not circumvent, at least rationally deal with this problem. It defines a weighted error function (i.e errors from each of the sensors are given weightage based on reliability) which is to be minimised.
The error function J can be simplified to a summation involving w_k (the weights, which are constants set by us) and the gain function g as defined below
It is easy to see that minimising J is equivalent to maximising g.
This expression when written in terms of quaternions becomes very compact. And qmethod showed that maximising g involved solving an eigenvalue problem. This can be done on MATLAB or other computer tools. But the solution is numerically intensive.[1] Satellite makers need a better algorithm than Q-method to determine the attitude with minimal compromise in the accuracy. The QuEST algorithm provides a less efficient but a ‘faster’ way to solve the eigenvalue problem.
QuEST starts with the assumption that sensor errors are minimal so that J can be minimised to a very low value. Rewriting J in terms of g,
where 
is the maximum eigenvalue of the K matrix defined in Q Method and Wahba's Problem.
With this can be written as
If we approximate J to be very small (this approximation is valid as we want to minimize J and now if after completing this method, we calculate J, it would be very small),
Defining and writing the equation in terms of Rodrigue’s parameter p simplifies the equation
where a is the vector along axis of rotation and Φ is the angle of rotation. Eigenvalue equation, which was to be solved is now written as
Which can be solved by gauss elimination.
Once the p has been obtained, the quaternion can be found out by noting
Hence the estimated quaternion is obtained without solving eigenvalue equation.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem