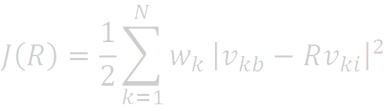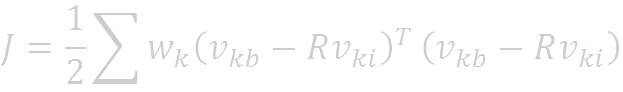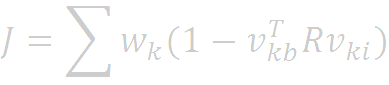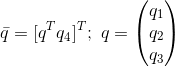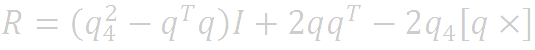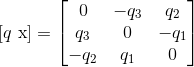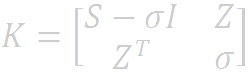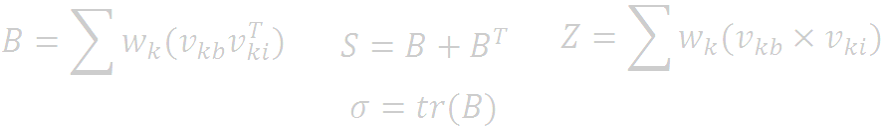Q Method and Wahba's Problem

TRIAD method is useful when we have only two vector measurements. If we need better accuracy and have more than two vector measurements, we need to use a more general algorithm. Before developing an algorithm, we need to make our problem statement more precise. Suppose we have a set of N unit vectors v_k, k = 1,2...N. For each vector, we have a sensor measurement in the body frame, v_{kb}, and a mathematical model of the components in the inertial frame, v_{ki}. We want to find a rotation matrix R_{bi}, such that

for each of the N vectors. Obviously this set of equations is overdetermined if N > 2, and therefore the equation cannot, in general, be satisfied for each k = 1,2..N. Thus we want to find a solution for R_{bi} that in some sense minimizes the overall error for the N vectors.

In this expression, J is the loss function to be minimized, k is the counter for the N observations, w_k is weight assigned to the kth measurement, v_{kb} is the matrix of measured components in the body frame, and vki is the matrix of components in the inertial frame as determined by appropriate mathematical models. This loss function is a sum of the squared errors for each vector measurement. If the measurements and0 mathematical models are all perfect, then the first equation on this page will be satisfied for all N vectors and J = 0. If there are any errors or noisy measurements, then J > 0. The smaller we can make J, the better the approximation of R_{bi}.

Q-Method

In this section we present one method to solve this minimization problem known as the Q-method. We first expand the loss function as

Assuming that the vectors are normalized we see that,

Defining,

We see that minimizing J is equivalent to maximizing g(R). This problem can be written in a more elegant way by representing rotation matrix R in terms of the quaternion

R can be written in terms of q as

Where [q x] is the cross product matrix associated with q

One can verify that the gain function in terms of the quaternions is:

Where K is a 4x4 Matrix given by

Wherein,

Now we want to maximise g, but noting that quaternion elements are not independent, but the constraint must also be satisfied. So we use lagrangian multiplier method and differentiate with respect to we get So now, the problem has been reduced to an eigenvalue problem for the matrix K. Since, K is a 4x4 matrix, it can have at most 4 different eigenvalues. Substituting in , we get

Now we want to maximise g. So we will chose the eigenvector corresponding to the maximum eigenvalue. Hence the estimated attitude can be known by solving the eigenvalue problem for the matrix K.
If you are done reading this page, you can go back to Attitude Determination and Control Subsystem

References

http://www.dept.aoe.vt.edu/~cdhall/courses/aoe4140/attde.pdf