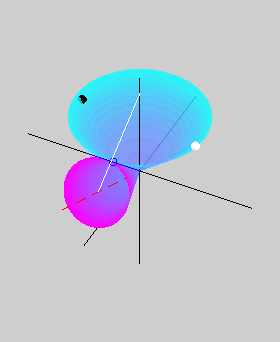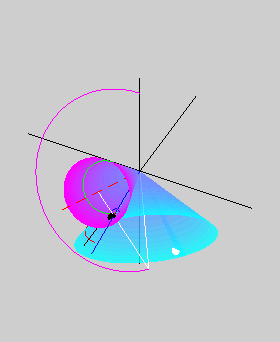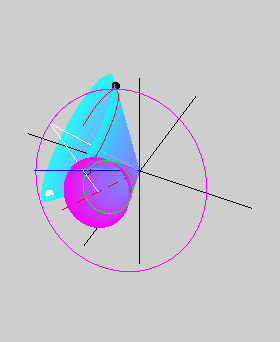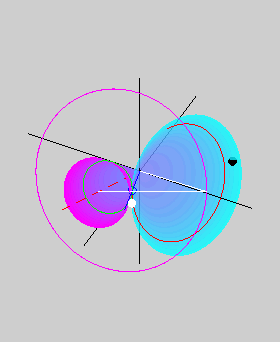Rotational Motion of an Axisymmetric Torque-Free Rigid Body

    The animations on this page depict the rotational motion of an axisymmetric body that rotates freely in the absence of any external torques. A body is said to be axisymmetric if any two of its three principal moments of inertia are equal. The axis corresponding to the third moment of inertia is called the axis of symmetry. Note that such a body may not appear axisymmetric to look at. In other words, the mass distribution may not be rotationally symmetric about the so called axis of symmetry. For instance, a homogeneous right prism with a square cross section will qualify as an axisymmetric body even though it does not possess rotational symmetry. The kinetic energy ellipsoid of an axisymmetric body is axisymmetric in the ordinary sense, that is, it is a surface of revolution and has rotational symmetry about the axis of symmetry.

    An axisymmetric body having the axis of symmetry as its minor principal axis is called prolate. A tall and thin cylinder is an example of a prolate body. The kinetic energy of a prolate axisymmetric body is symmetric about its
longest geometric axis. The animation on the right shows the kinetic energy ellipsoid of a prolate axisymmetric body rolling without slipping on the invariant plane as the body rotates. A comparison with similar simulations of a rotating asymmetric body shows that the rotational motion of an axisymmetric body is smoother and more regular. This is because, in the axisymmetric case, the kinetic energy ellipsoid has circular cross sections.

    The green circle shows the tip of the angular velocity vector. As the body rotates, an inertial observer sees the angular velocity vector tracing out the herpolhode shown in yellow. However, an observer rotating with the body sees the same angular velocity vector tracing out the polhode shown in red. The pink curve shows the path traced out by a point on the minor principal axis of inertia.
Unlike in the asymmetric case, all three curves are circles, and the minor principal axis, which is the symmetry axis for a prolate body, exhibits only precession without any nutation.

    An axisymmetric body is called oblate if its axis of symmetry is its major principal axis of inertia. A short, fat circular cylinder is an example of an oblate axisymmetric body. The kinetic energy ellipsoid of an oblate body is symmetric
about its shortest geometrical axis. The simulation on the left shows the kinetic energy ellipsoid of an oblate axisymmetric body rolling without slipping on the invariant plane as the body rotates. As in the prolate case, the herpolhode (in yellow) and the polhode (in red) are circular.

    Both the animations above show that the angular velocity vector (the blue segment) of an axisymmetric body traces out a cone in the body frame. This cone, called the body cone, intersects the kinetic energy elliposid in the polhode and has the symmetry axis as its axis. The angular velocity vector also traces out a cone as seen by an inertial observer. The axis of this space cone is along the angular momentum vector (dashed red line), and its intersection with the invariant plane is the herpolhode. While the space cone remains stationary with respect to an inertial observer, the body cone moves such that the line of contact between the two cones is along the angular velocity vector. Since material points in the body that lie along the angular velocity vector are instantaneously stationary with respect to the inertial frame, it follows that the body cone rolls without slipping on the space cone as the axisymmetric body rotates. This motion of the body cone thus provides an alternative geometric description of the rotational motion in the special case of an axisymmetric body.

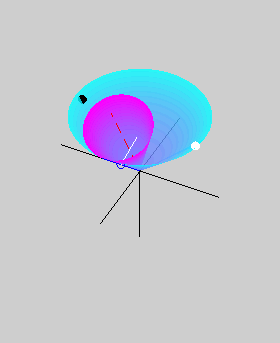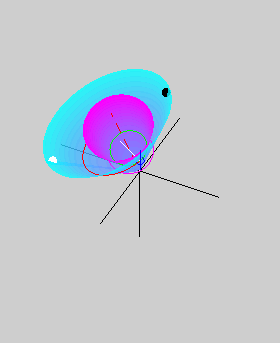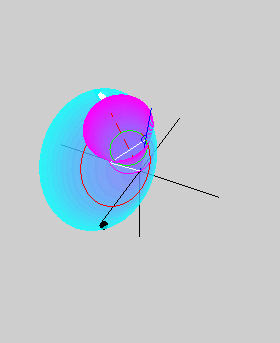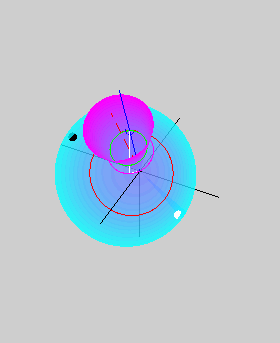
    The  two animations below show the body cone (in cyan) rolling on the space cone (in magenta) without slipping. The animation on the left is for a prolate body, while that on the right is for an oblate body. The red dashed line shows the angular momentum vector, which is also the axis of the space cone. The axis of the body cone, which is also the axis of symmetry, is shown in white. The pink curve is the path of a point on the axis of symmetry. The small blue circle shows the tip of the angular velocity vector lying along the line of contact of the two cones. The tip of the angular velocity vector traces out the green herpolhode on the space cone as well as the red polhode on the body cone. The blue circle also lies along the white line joining the angular momentum vector and the axis of symmetry, thus showing that the angular momentum vector, the angular velocity vector, and the axis of symmetry all lie in the same plane (could you observe this in the two animations above?). However, while the angular velocity vector lies between the other two in the prolate case, it is the angular momentum vector that lies in between in the oblate case. Consequently, the space cone lies outside the body cone in the prolate case, but inside it in the oblate case. This difference gives rise to prograde and retrograde precession in the prolate and oblate cases, respectively. The black and white circles on the body cone are meant to help visualize the rotational motion of the body cone better.



 












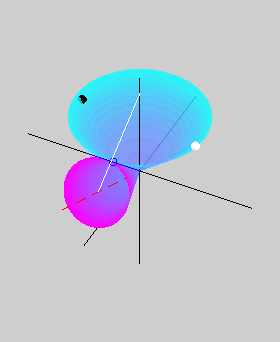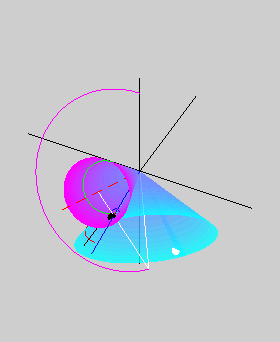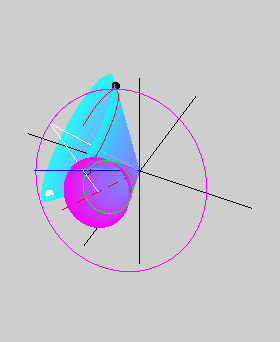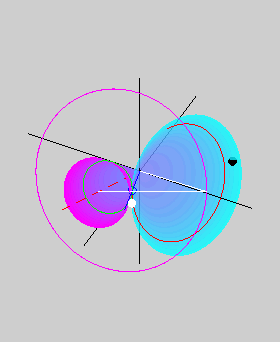
                                                                                                                                                                                                                                                   The animations appearing on this page were created with the help of Debashish Bagg.